Regresiones lineales, predictores categóricos y representación gráfica
0. Objetivo de la práctica
El objetivo del práctico, es avanzar en el análisis de los datos a través del uso de regresiones lineales, para esto usaremos datos previamente procesados de la base de datos a utilizar. Recordemos que estamos en el proceso de análisis

Entonces, en esta práctica aprenderemos trabajar las regresiones lineales, también trabajaremos los predictores categóricos y finalmente veremos como representarlos mediante gráficos y tablas.
1. Recursos del práctico
En este práctico utilizamos los datos procesados de la Encuesta Suplementaria de Ingresos (ESI) 2020.Recuerden siempre consultar el libro códigos antes de trabajar datos.
- [<i class="fas fa-file-archive"></i> `06-bloque.zip`](https://github.com/learn-R/09-class/raw/main/06-bloque.zip)
2. Librerías a utilizar
Cargaremos los paquetes con pacman revisar práctico 3 y utilizaremos sjPlot para la creación de tablas, tidyverse de este universo de paquetes utilizaremos dplyr (para la manipulación de datos) y magrittr (para utilizar el operador pipe) y finalmente la libreria car para la recodificación de datos. Recuerden que pueden ver más de las funciones de cada paquetes en la sección de recursos
pacman::p_load(sjPlot,
tidyverse,
magrittr,
car)
3. Importar datos
Una vez cargado los paquetes a utilizar, debemos cargar los datos procesados.
load("output/data/datos_proc.RData")
Explorar datos
Es relevante explorar los datos que utilizaremos, cómo están previamente procesados ¡no sabemos con que variables estamos trabajando!
names(datos_proc)
## [1] "ingresos" "educacion" "sexo" "edad"
head(datos_proc)
## # A tibble: 6 x 4
## ingresos educacion sexo edad
## <dbl> <dbl+lbl> <dbl+lbl> <dbl>
## 1 320421. 6 [Educación técnica (Educación superior no universi~ 2 [Mujer] 29
## 2 750000 7 [Educación universitaria] 2 [Mujer] 30
## 3 900000 7 [Educación universitaria] 2 [Mujer] 43
## 4 0 5 [Educación secundaria] 2 [Mujer] 15
## 5 0 3 [Educación primaria (nivel 1)] 1 [Hombr~ 11
## 6 0 5 [Educación secundaria] 2 [Mujer] 62
Ahora sabemos que trabajaremos con "ingresos", "educacion", "sexo" y "edad". Inclusive podemos repasar lo visto en el práctico anterior y explorar nuestros datos con sjPlot::view_df()
sjPlot::view_df(datos_proc,
encoding = "UTF-8")
| ID | Name | Label | Values | Value Labels |
|---|---|---|---|---|
| 1 | ingresos | Total ingresos sueldos y salarios | range: 0.0-9312239.1 | |
| 2 | educacion | Clasificación Internacional de Nivel Educacional (CINE) |
1 2 3 4 5 6 7 8 9 999 |
Nunca estudió Educación preescolar Educación primaria (nivel 1) Educación primaria (nivel 2) Educación secundaria Educación técnica (Educación superior no universitaria) Educación universitaria Postitulos y maestrÃa Doctorado Nivel ignorado |
| 3 | sexo | Sexo | 1 2 |
Hombre Mujer |
| 4 | edad | Edad de la persona | range: 0-106 | |
Pero previo a eso podemos visualizar que hay categorías que se pueden reducir en la variable educacion, por eso haremos un breve repaso del práctico anterior
Recodificar
Como la variable educacion presenta la categoría de respuesta Nivel ignorado (casos perdidos) y casos que pueden unificarse como Educación primaria (nivel 1) y Educación primaria (nivel 2), los asignaremos como NA y unificaremos.
Para eso el primer paso es decirle a la base que transformaremos la variable como factor
datos_proc$educacion <- as_factor(datos_proc$educacion)
Luego recodificaremos la variable con la función recode del paquete car
datos_proc$educacion <- car::recode(datos_proc$educacion, recodes = c("'Nivel ignorado' = NA;
c('Educación primaria (nivel 1)', 'Educación primaria (nivel 2)') = 'Educación primaria'"))
Finalmente visualizamos los cambios de nuestra base procesada con view_df
| ID | Name | Label | Values | Value Labels |
|---|---|---|---|---|
| 1 | ingresos | Total ingresos sueldos y salarios | range: 0.0-9312239.1 | |
| 2 | educacion | Doctorado Educación preescolar Educación primaria Educación secundaria Educación técnica (Educación superior no universitaria) Educación universitaria Nunca estudió Postitulos y maestrÃa |
||
| 3 | sexo | Sexo | 1 2 |
Hombre Mujer |
| 4 | edad | Edad de la persona | range: 0-106 | |
Perfecto, podemos ver las variables que tenemos y sus categorías de respuesta, pero antes de continuar, es importante conocer los tipos de variables a usar, para eso pueden ir al mini tutorial de tipos de variables y ejemplos
4. Modelo de regresión
Previo al trabajo en R recordemos que la fórmula de la regresión lineal simple es:
\begin{equation} \widehat{Y}=b_{0} +b_{1}X \end{equation}
Mientras que en la regresión lineal múltiple es:
\begin{equation} \widehat{Y}=b_{0} +b_{1}X +b_{2}X +b_{x}X \end{equation}
Donde
\(\widehat{Y}\)es el valor estimado/predicho de\(Y\)\(b_{0}\)es el intercepto de la recta (el valor de Y cuando las X’s son 0)\(b_{1}\)y\(b_{2}\)son los coeficientes de regresión, que nos dice cuánto aumenta Y por cada punto que aumenta X (pendiente)
Les mostramos esto porque de la misma forma se diferencian ambos procedimientos en R
Para la regresión lineal simple se utiliza la siguiente estructura:
objeto <- lm(dependiente ~ independiente, data=datos)
Mientras que para la regresión lineal múltiple, sólo se añaden más variables
objeto <- lm(dependiente ~ independiente1 + independiente 2 + independientex, data=datos)
Regresión lineal simple
Ahora en nuestros datos queda de la siguiente manera
reg_1 <-lm((ingresos ~ edad), data = datos_proc)
reg_1
##
## Call:
## lm(formula = (ingresos ~ edad), data = datos_proc)
##
## Coefficients:
## (Intercept) edad
## 102548 1530
pero el problema es que al observar el objeto creado, no es muy presentable para informes, por eso usaremos la función tab_model de sjPlot, que tiene la siguiente estructura:
sjPlot::tab_model(objeto_creado,
show.ci= F/T, # este argumento muestra los intervalos de confianza
encoding = "UTF-8", # evita errores en caracteres
file = "output/figures/reg1_tab.doc") # guarda lo creado automáticamente
Ahora en nuestros datos se vería así:
sjPlot::tab_model(reg_1, show.ci=FALSE, encoding = "UTF-8", file = "output/figures/reg1_tab.doc")
| Total ingresos sueldos y salarios |
||
|---|---|---|
| Predictors | Estimates | p |
| (Intercept) | 102548.34 | <0.001 |
| Edad de la persona | 1529.88 | <0.001 |
| Observations | 71935 | |
| R2 / R2 adjusted | 0.007 / 0.007 | |
Regresión múltiple
Ahora queremos incorporar las demás variables al modelo, para lo haremos de la siguiente manera
reg_2 <-lm((ingresos ~ edad + sexo), data = datos_proc)
sjPlot::tab_model(reg_2, show.ci=FALSE, encoding = "UTF-8", file = "output/figures/regnc_tab.doc")
| Total ingresos sueldos y salarios |
||
|---|---|---|
| Predictors | Estimates | p |
| (Intercept) | 237220.44 | <0.001 |
| Edad de la persona | 1646.83 | <0.001 |
| Sexo | -91039.16 | <0.001 |
| Observations | 71935 | |
| R2 / R2 adjusted | 0.020 / 0.020 | |
¡Pero espera! ¡sexo no es una variable continua!
Predictores categoricos
Previo a esto hay que recordar que sexo no es un predictor continuo, y también debemos recordárselo a la base de datos (la variable educación tampoco lo es, pero ya la transformamos con as_factor)
datos_proc$sexo <- as_factor(datos_proc$sexo)
Perfecto ahora si podemos añadir predictores categóricos a nuestra regresión múltiple
reg_2 <-lm((ingresos ~ edad + sexo), data = datos_proc)
reg_3 <-lm((ingresos ~ edad + sexo + educacion), data = datos_proc)
Pero que pasa si queremos incluir todos los modelos creados en una sola tabla, para eso usaremos nuevamente la función tab_model de sjPlot
sjPlot::tab_model(list(reg_1, reg_2, reg_3), # los modelos estimados
show.ci=FALSE, # no mostrar intervalo de confianza (por defecto lo hace)
p.style = "stars", # asteriscos de significación estadística
dv.labels = c("Modelo 1", "Modelo 2", "Modelo 3"), # etiquetas de modelos o variables dep.
string.pred = "Predictores", string.est = "β", # nombre predictores y símbolo beta en tabla
encoding = "UTF-8",
file = "output/figures/reg_tab_all.doc")
| Modelo 1 | Modelo 2 | Modelo 3 | |
|---|---|---|---|
| Predictores | ß | ß | ß |
| (Intercept) | 102548.34 *** | 146181.28 *** | 1774294.45 *** |
| Edad de la persona | 1529.88 *** | 1646.83 *** | 1134.98 *** |
| Sexo: Mujer | -91039.16 *** | -94042.51 *** | |
| educacion: Educación preescolar |
-1734569.27 *** | ||
| educacion: Educación primaria |
-1732259.96 *** | ||
| educacion: Educación secundaria |
-1632080.40 *** | ||
| educacion: Educación técnica(Educación superior no universitaria) |
-1497544.27 *** | ||
| educacion: Educación universitaria |
-1342780.60 *** | ||
| educacion: Nunca estudió | -1743566.17 *** | ||
| educacion: Postitulos y maestrÃa |
-641544.23 *** | ||
| Observations | 71935 | 71935 | 71346 |
| R2 / R2 adjusted | 0.007 / 0.007 | 0.020 / 0.020 | 0.202 / 0.201 |
| * p<0.05 ** p<0.01 *** p<0.001 | |||
Ahora podemos observar que a diferencia de la tabla anterior la variable sexo, tiene incluida la categoría de respuesta de comparación.
5. Visualización
Para visualizar o graficar los coeficientes de regresión para poder observar el impacto de cada variable en el modelo utilizaremos la función plot_model de sjPlot, su estructura es la siguiente:
sjPlot::plot_model(objeto_creado,
ci.lvl = "", #estima el nivel de confianza
title = "", # es el título
vline.color = "") # color de la recta vertical
Esto visualizado con nuestro modelo se ve así:
sjPlot::plot_model(reg_3, ci.lvl = c(0.95), title = "Estimación de predictores", vline.color = "purple")
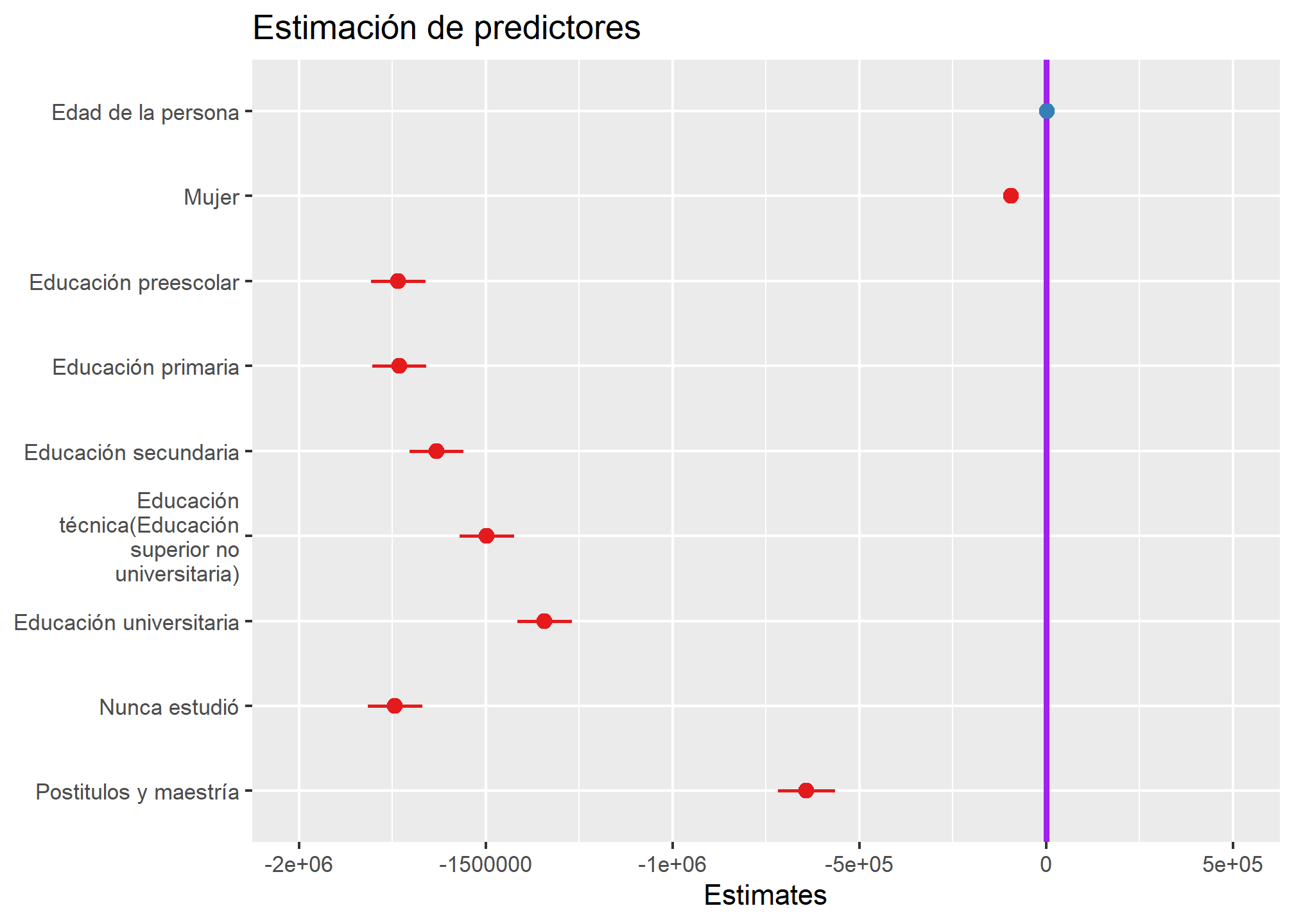
Terminamos por este práctico ¡Pero aún falta la regresión logística!
6. Resumen
En este práctico aprendimos a
- Crear y visualizar regresiones lineales
- Incorporar predictores categóricos
- Crear y visualizar regresiones múltiples
7. Recursos
8. Reporte de progreso
¡Recuerda rellenar tu reporte de progreso. En tu correo electrónico está disponible el código mediante al cuál debes acceder para actualizar tu estado de avance del curso.