Descriptivos
0. Objetivo del práctico
El objetivo del práctico, es avanzar en el análisis de los datos a través del uso de estadísticos descriptivos. Para esto ya debemos contar con datos previamente procesados del práctico N°3. Recordemos en qué parte del proceso estamos

En este práctico veremos tanto la estimación puntual de estadísticos descriptivos, como su visualización para reportes, ya sea a través de tablas o de gráficos.
Recursos del práctico
En este práctico utilizamos los datos procesados CASEN 2020, que proviene de los datos originales de Encuesta de Caracterización Socioeconómica (CASEN).Recuerden siempre consultar el libro códigos antes de trabajar datos.
1. Paquetes a utilizar
Para este práctico utilizaremos principalmente, las librerías sjmisc y sjPlot.
sjmisc: esta paquete tiene múltiples funciones, desde la transformación de datos y variables. Este paquete suele complementar a dplyr de tidyverse en sus funciones.
sjPlot: su principal función es la visualización de datos para estadística en ciencias sociales mediante tablas y gráficos.
Cargaremos los paquetes con pacman revisar práctico anterior
pacman::p_load(sjmisc,
sjPlot,
tidyverse,
magrittr)
theme_set(theme_sjplot2())
2. Importar datos
Una vez cargado los paquetes a utilizar, debemos pasar al segundo paso: cargar los datos. Como indicamos al inicio, seguiremos utilizando los datos *CASEN que fue procesada en el práctico anterior, pero le añadimos una variable.
load("output/data/datos_proc.RData")
3. Explorar datos
Pero ¿cómo sabremos cuales son las variables que componen la base de datos procesada?, para ello usaremos dos códigos para conocer la base procesada que usaremos:
el código names, nos entrega los nombres de las variables que componen el data set
names(datos_proc)
## [1] "sexo" "edad_tramo" "ocupacion"
## [4] "horas_mens" "ingreso_percapita" "ife"
Mientras que la función head nos entrega el nombre y las primeras 10 filas que la componen.
head(datos_proc)
## # A tibble: 6 x 6
## sexo edad_tramo ocupacion horas_mens ingreso_percapita ife
## <dbl+lbl> <chr> <fct> <dbl> <dbl> <dbl+lbl>
## 1 2 [Mujer] Joven No NA 195416. 1 [Sí]
## 2 1 [Hombre] Adulto Sí 180 315861 2 [No]
## 3 2 [Mujer] Joven No NA 315861 2 [No]
## 4 1 [Hombre] Adulto Sí 45 1001389 2 [No]
## 5 1 [Hombre] Joven No NA 1001389 2 [No]
## 6 2 [Mujer] Adulto No NA 1001389 2 [No]
Gracias a estos códigos sabemos que tenemos una aproximación de las variables que podríamos utilizar. Por el práctico anterior sabemos que podemos explorar nuestros datos con sjPlot::view_df()
| ID | Name | Label | Values | Value Labels |
|---|---|---|---|---|
| 1 | sexo | Sexo | 1 2 |
Hombre Mujer |
| 2 | edad_tramo | <output omitted> | ||
| 3 | ocupacion | o1. La semana pasada, ¿trabajó al menos una hora? | Sà No |
|
| 4 | horas_mens | y2_hrs. Número de horas mensuales pactadas con empleador |
range: 1-720 | |
| 5 | ingreso_percapita | Ingreso total del hogar | range: 0.0-225200000.0 | |
| 6 | ife | y26d_hog. Últimos 12 meses, ¿alguien recibió Ingreso Familiar de Emergencia? |
1 2 9 |
SÃ No No sabe |
4. Descripción de variables
Una vez conocidas las variables que incluye nuestros datos procesados, ¿cómo podemos realizar un análisis descriptivo para algún informe o reporte? Veamos algunas de las más comunes
4.1. Medidas de tendencia central
Para conocer las medidas de tendencia central de las variables hay dos opciones. En la primera se puede pedir el estadístico manualmente, en la segunda se puede pedir una tabla resumen.
Media
Para conocer la media de una variable se utiliza la función mean(), su estructura es:
mean(datos$variable, na.rm=TRUE)
El argumento na.rm=TRUE excluye del cálculo a los casos perdidos. Esto aplicado a nuestra variable ingreso_percapita se ve así:
mean(datos_proc$ingreso_percapita, na.rm=TRUE)
## [1] 355472.1
Media recortada
Pero, ¿qué pasa si la variable ingreso_percapita esta influenciada por casos influyentes? Para eso puedo pedir la media recortada agregando el argumento trim para excluir al 5% de cada extremo
mean(datos_proc$ingreso_percapita, na.rm=TRUE, trim = 0.025)
## [1] 305707.9
Aquí podemos ver que el valor es distinto.
Ya conocimos el promedio de la variable ingreso_percapita podemos informar cuanto es el promedio del ingreso en el hogar en Chile, pero antes de eso queremos saber ¿cuánto gana el 50% de los hogares? Para eso calcularemos la mediana
Mediana
Para el cálculo de la mediana se utiliza el comando median, su estructura es similar a la mean():
median(datos$variable, na.rm =TRUE)
median(datos_proc$ingreso_percapita, na.rm =TRUE)
## [1] 229184.5
Ahora ya sabemos que al menos un 50% de las familias en Chile tienen por ingreso $229.184.
Ya tenemos los estadísticos principales, pero ¿cómo los reportamos? ¿tenemos que sacar el promedio de cada variable una por una? ¡No!, para ello sjmisc tiene diferentes funciones, que veremos a continuación
Un resumen
Podemos obtener un resumen de todos estadísticos a partir de la función summary(). El argumento puede ser tanto una columna en particular como ingreso_percapita
summary(datos_proc$ingreso_percapita)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0 138612 229184 355472 390890 225200000
También podemos hacerlo con todos los datos. Sólo que no tendrá mucho sentido para las variables nominales.
summary(datos_proc)
## sexo edad_tramo ocupacion horas_mens
## Min. :1.000 Length:144418 Sí:60479 Min. : 1.0
## 1st Qu.:1.000 Class :character No:83939 1st Qu.:146.0
## Median :2.000 Mode :character Median :180.0
## Mean :1.547 Mean :152.8
## 3rd Qu.:2.000 3rd Qu.:180.0
## Max. :2.000 Max. :720.0
## NA's :111080
## ingreso_percapita ife
## Min. : 0 Min. :1.000
## 1st Qu.: 138612 1st Qu.:1.000
## Median : 229184 Median :2.000
## Mean : 355472 Mean :1.766
## 3rd Qu.: 390890 3rd Qu.:2.000
## Max. :225200000 Max. :9.000
##
summary() es una función muy potente, dado que no solo permite resúmenes de data.frames (datos), sino que también de otros objetos en R (como los modelos).
Ahora bien tiene limitantes para interactuar con dplyr y generar archivos de salida. Por ello ocuparemos descr de sjmisc
sjmisc::descr(datos_proc$ingreso_percapita,
show = "all",
out = "viewer",
encoding = "UTF-8",
file = "output/figures/tabla-ingreso.doc")
##
## ## Basic descriptive statistics
##
## var type label n NA.prc mean sd se
## dd numeric Ingreso total del hogar 144418 0 355472.2 834151.2 2195
## md trimmed range iqr skew
## 229184.5 266168.1 225200000 (0-225200000) 252277.6 152.42
De más variables
datos_proc %>%
select(ingreso_percapita, horas_mens) %>%
sjmisc::descr(
show = "all",
out = "viewer",
encoding = "UTF-8",
file = "output/figures/tabla1.doc")
##
## ## Basic descriptive statistics
##
## var type
## ingreso_percapita numeric
## horas_mens numeric
## label n NA.prc
## Ingreso total del hogar 144418 0.00
## y2_hrs. Número de horas mensuales pactadas con empleador 33338 76.92
## mean sd se md trimmed range iqr
## 355472.15 834151.23 2195.0 229184.5 266168.13 225200000 (0-225200000) 252277.6
## 152.83 54.69 0.3 180.0 159.83 719 (1-720) 34.0
## skew
## 152.42
## -0.98
Aquí podemos ver la variable var, el tipo de variable type, su etiqueta label, los casos válidos n, los casos perdidos NA.prc, las medidas de tendencia central y las de dispersión. sjmisc tiene muchos beneficios, ya que cómo interactúa con el mundo tidyverse es fácil de complementar con funciones como select de dplyr. Además con la función file se puede exportar automáticamente la tabla para los reportes.
4.3. Frecuencias
Frecuencias absolutas
Para conocer las frecuencias absolutas de una variable se podría usar la función table, esta nos arroja la frecuencia por cada categoría de respuesta
table(datos_proc$sexo)
##
## 1 2
## 65474 78944
También podríamos usar la función flat_table, esta puede agrupar más variables y agruparlas.
flat_table(datos_proc, sexo, ocupacion, ife)
## ife Sí No No sabe
## sexo ocupacion
## Hombre Sí 9695 23979 473
## No 11263 19571 493
## Mujer Sí 7527 18488 317
## No 20084 31701 827
El problema es ¿cómo podríamos reportarla en nuestros informes? Si queremos una tabla general usaremos la función frq. Esta función devuelve una tabla de frecuencias de vectores etiquetados, como marco de datos.
sjmisc::frq(datos_proc$sexo,
out = "viewer",
title = "Frecuencias",
encoding = "UTF-8",
file = "output/figures/tabla2.doc")
| val | label | frq | raw.prc | valid.prc | cum.prc | |
|---|---|---|---|---|---|---|
| 1 | Hombre | 65474 | 45.34 | 45.34 | 45.34 | |
| 2 | Mujer | 78944 | 54.66 | 54.66 | 100.00 | |
| NA | NA | 0 | 0.00 | NA | NA | |
| total N=144418 · valid N=144418 · x̄=1.55 · σ=0.50 | ||||||
5. Visualización
Ahora que ya sabemos como tener todos los estadísticos necesarios para escribir nuestros reportes, viene el segundo paso visualizar los estadísticos. Esto lo haremos con sjPlot
Para visualizar las frecuencias usaremos la función plot_frq, su estructura es la siguiente:
plot_frq(datos, #base
..., #variable
title = "", # título
type = c("bar", "dot", "histogram", "line", "density", "boxplot", "violin") #tipo de gráfico
Para los gráficos, tenemos los siguientes códigos
5.1. Gráfico de barras de frecuencias simple
Si quisiéramos presentar gráficos que entreguen la frecuencia de cada categoría de respuesta, podemos presentarla de la siguiente forma:
plot_frq(datos_proc, edad_tramo,
title = "Gráfico de frecuencias, barras",
type = c("bar"))
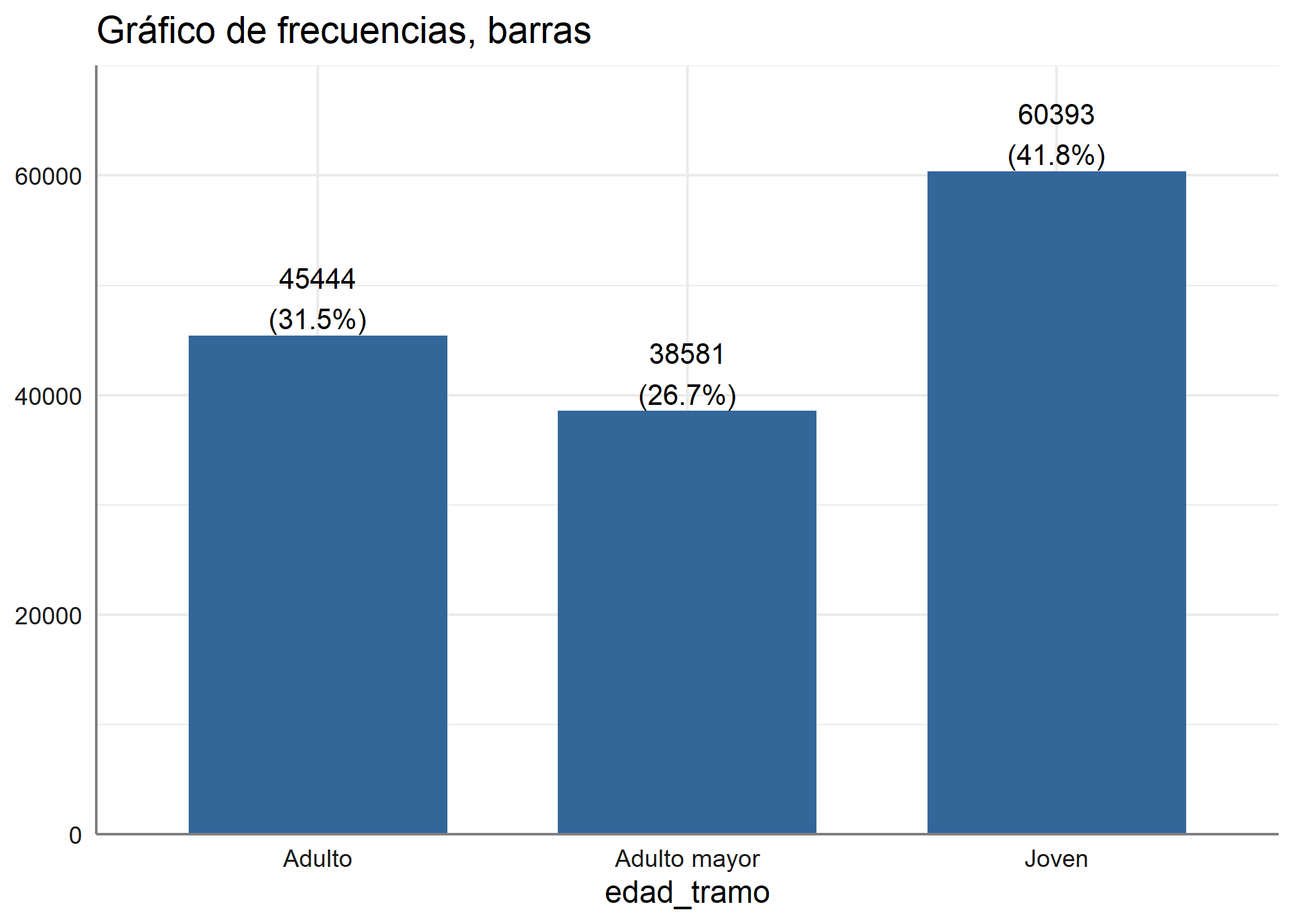
Además de la visualización es importante el guardar los datos que se producen y sjPlot tiene su propio código para hacerlo a través de la función save_plot(), su estructura es esta:
save_plot(last_plot()) #se deja el formato del archivo (.png, .jpg, .svg o .tif) y la ruta de la carpeta
Así guardaríamos el gráfico anterior
save_plot(last_plot("/output/img/tab.png"))
5.2. Gráfico de puntos
Si tenemos más categorías y queremos mejorar el reporte, podemos usar este código:
plot_frq(datos_proc, edad_tramo,
title = "Gráfico de frecuencias, puntos",
type = c("dot"))
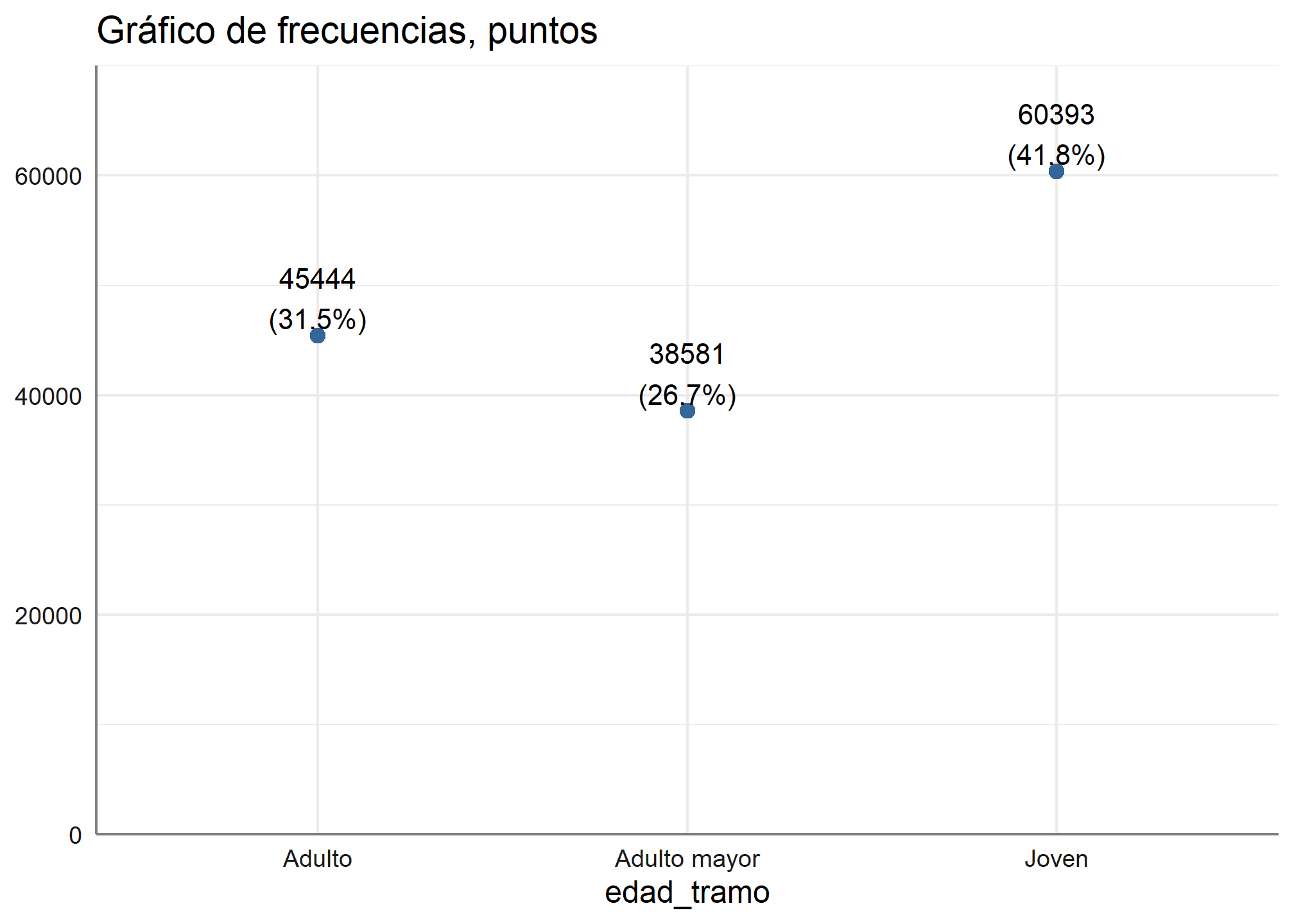
También podemos cambiar el orden del eje x e y
plot_frq(datos_proc$edad_tramo, type = "dot", show.ci = TRUE, sort.frq = "desc",
coord.flip = TRUE, expand.grid = TRUE, vjust = "bottom", hjust = "left", title = "Gráfico de frecuencias, puntos cambiado"
)
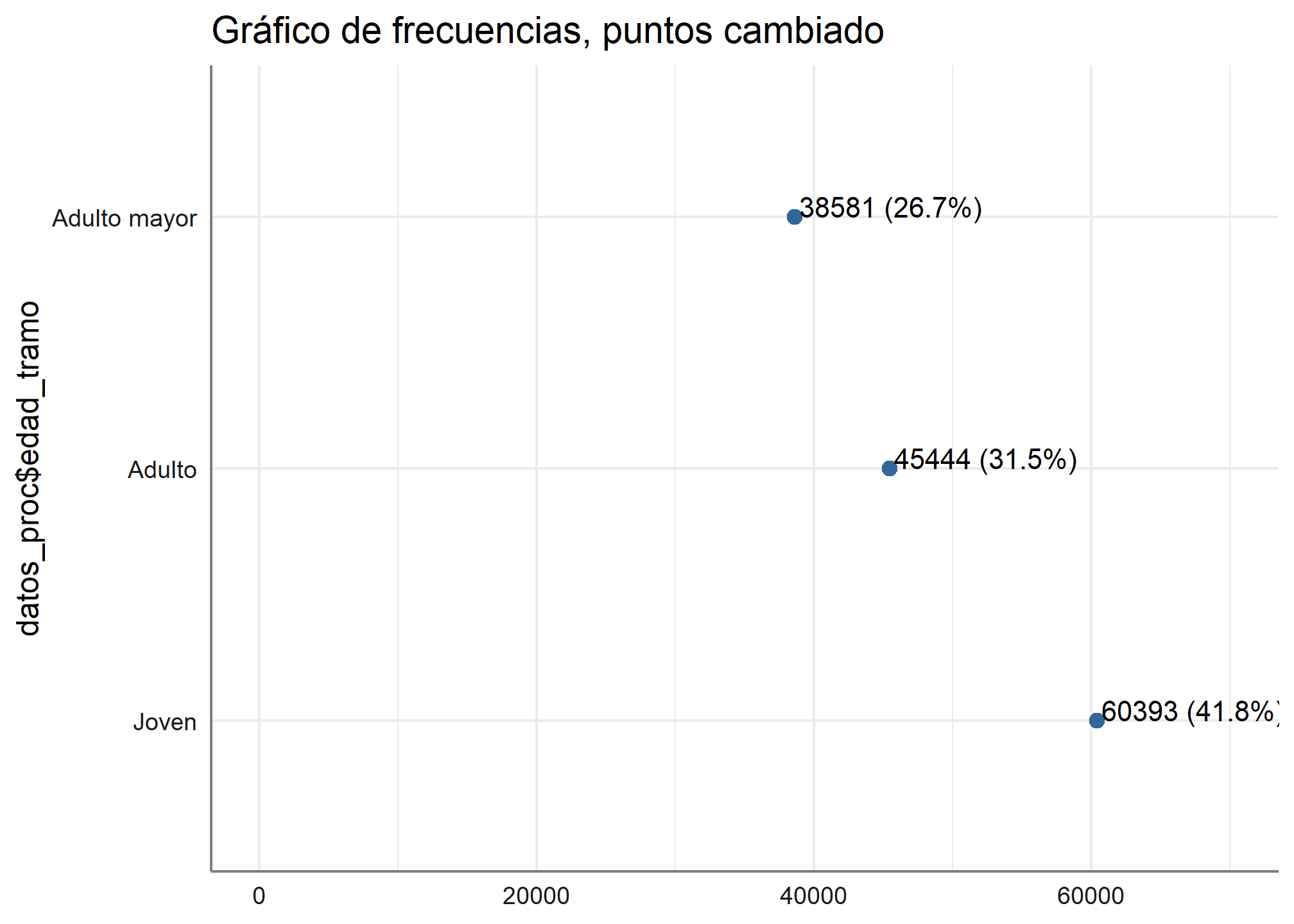
5.3 Histogramas
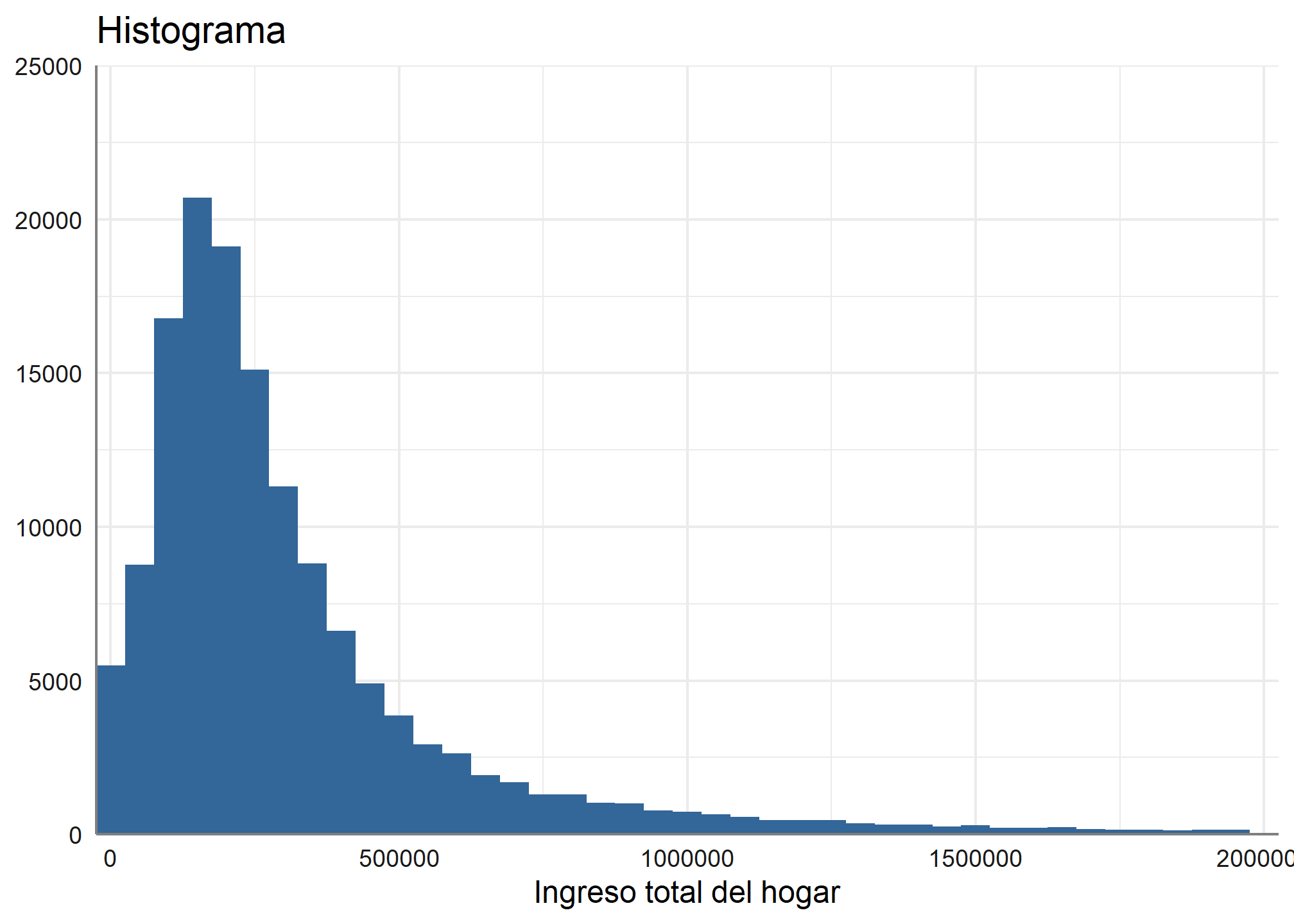
Otra función que podemos hacer es graficar histogramas, sin embargo, como ya hemos visto, la variable ingreso_percapita tiene casos muy altos que distorsionan la variable. Para solucionar esto, ocuparemos lo aprendido en el práctico anterior y filtraremos la variable sacando los ingresos mayores a $2.000.000, con la función filter de dplyr
datos_proc %>% filter(ingreso_percapita <= 2000000) %>%
plot_frq(., ingreso_percapita,
title = "Histograma",
type = c("histogram"))
5.4 Densidad
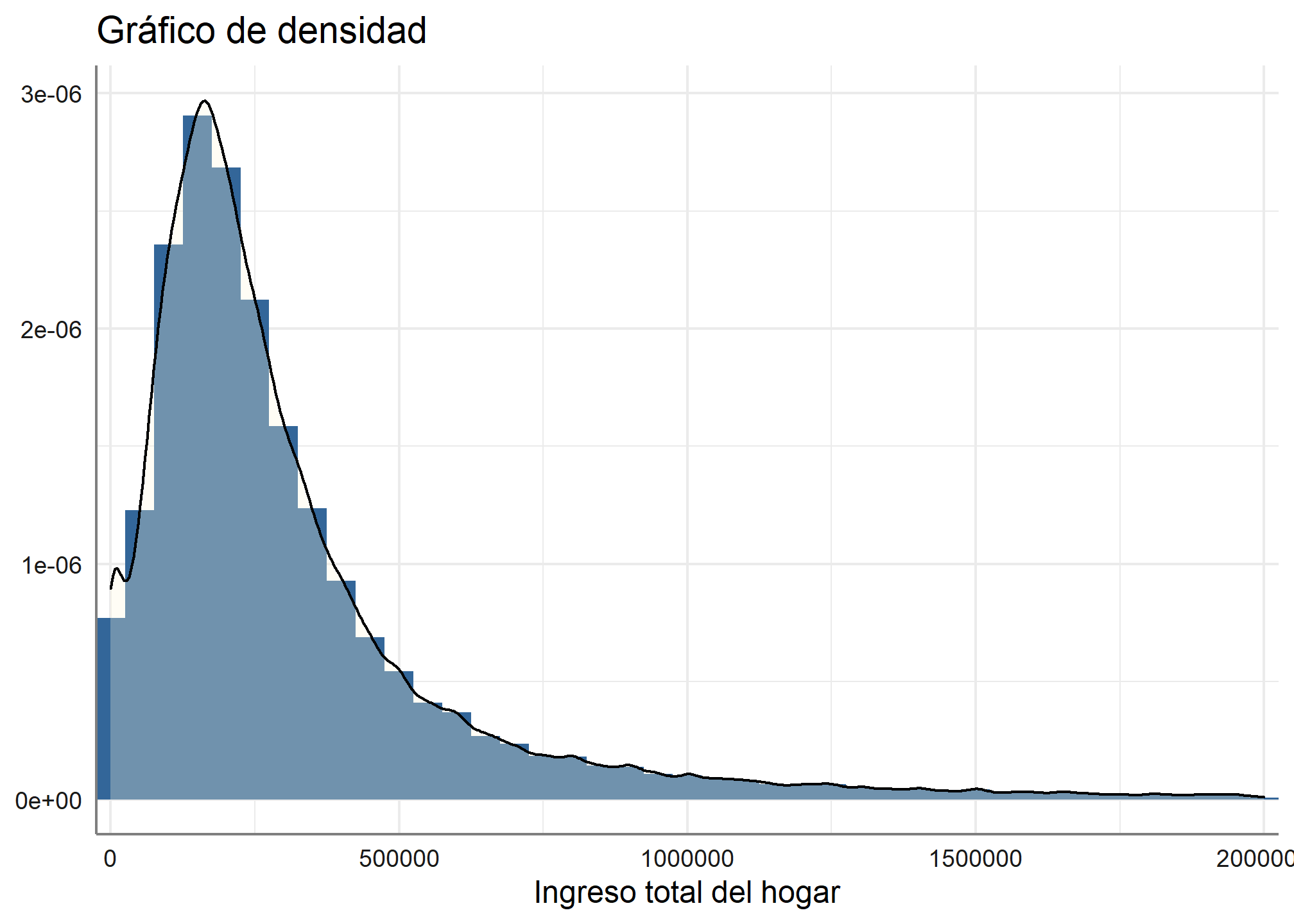
Ahora que vemos la distribución del histograma, ¿cómo podemos ver su densidad?, es muy simple, para ello haremos un gráfico de densidad con el siguiente código
datos_proc %>% filter(ingreso_percapita <= 2000000) %>%
plot_frq(., ingreso_percapita,
title = "Gráfico de densidad",
type = c("density"))
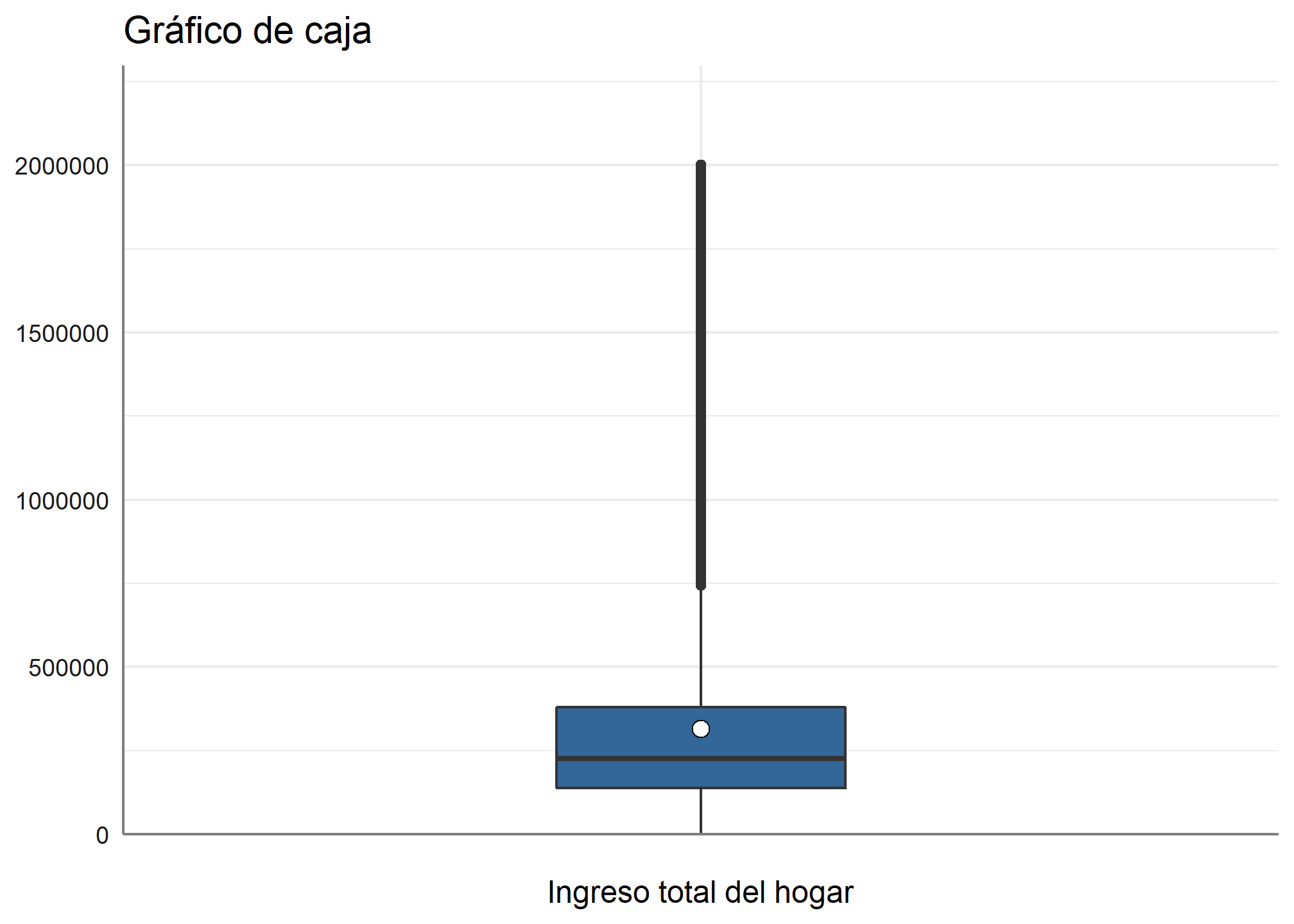
5.5 Gráfico de cajas
Para graficar los estadísticos de una variable, podemos hacerlo a través de un gráfico de cajas, para ello usaremos este código:
datos_proc %>% filter(ingreso_percapita <= 2000000) %>%
plot_frq(., ingreso_percapita,
title = "Gráfico de caja",
type = c("boxplot"))
5.6 Gráfico de violín
Finalmente, si queremos presentar gráficos de violín, usamos este código
datos_proc %>% filter(ingreso_percapita <= 2000000) %>%
plot_frq(., ingreso_percapita,
title = "Gráfico de violín",
type = c("violin"))
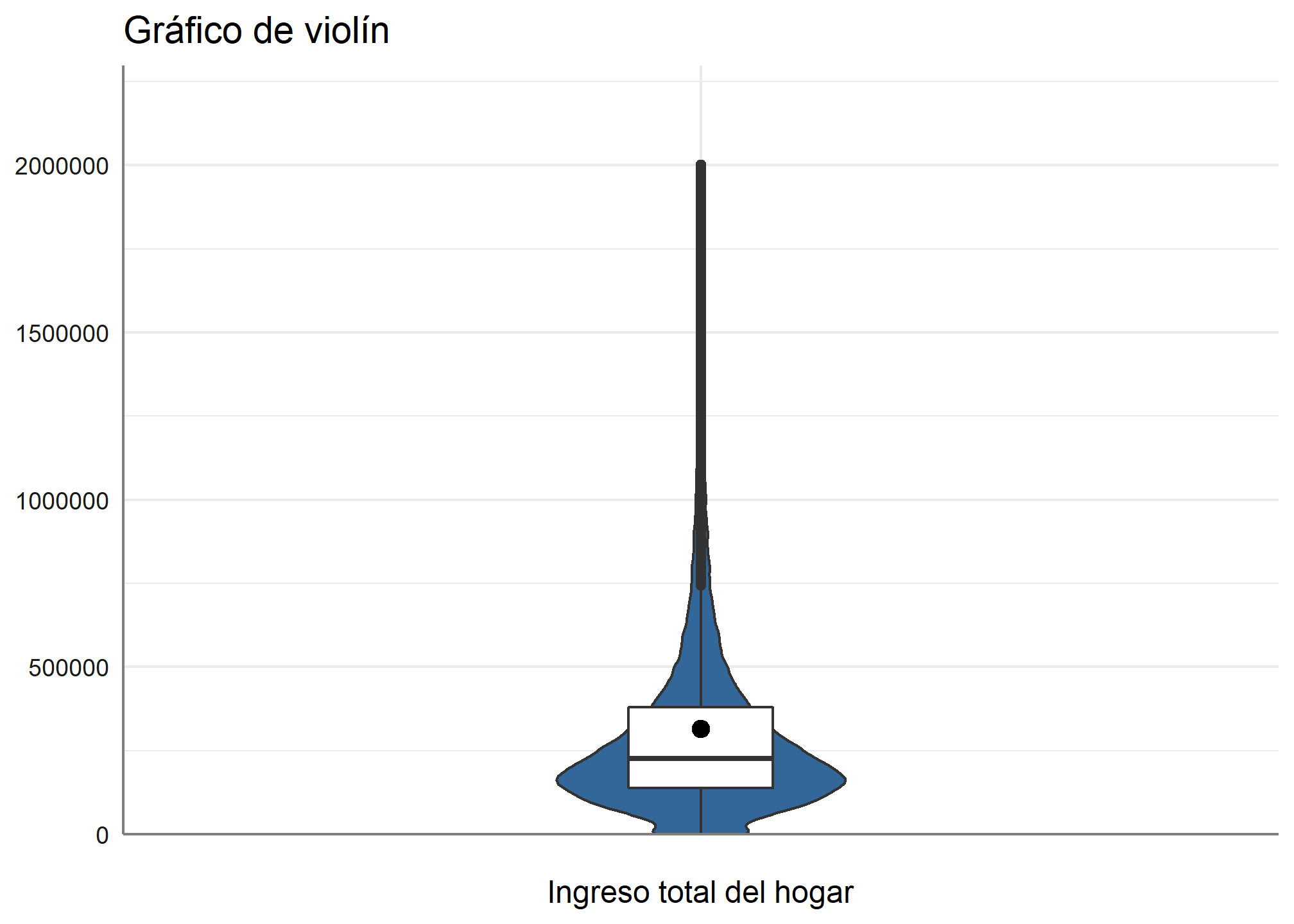
Como pueden ver, el único argumento que se modificaba era type = , es decir, para hacer diversos gráficos, sólo se debe especificar el tipo de gráfico que queremos.
5.7 Gráfico de nube de puntos
Ahora, si quisiéramos graficar la distribución de dos variables, podemos hacerlo con la función plot_scatter, esta muestra el diagrama de dispersión de dos variables.
datos_proc %>%
filter(ingreso_percapita <= 2000000, horas_mens <= 600) %>%
plot_scatter(., horas_mens, ingreso_percapita)
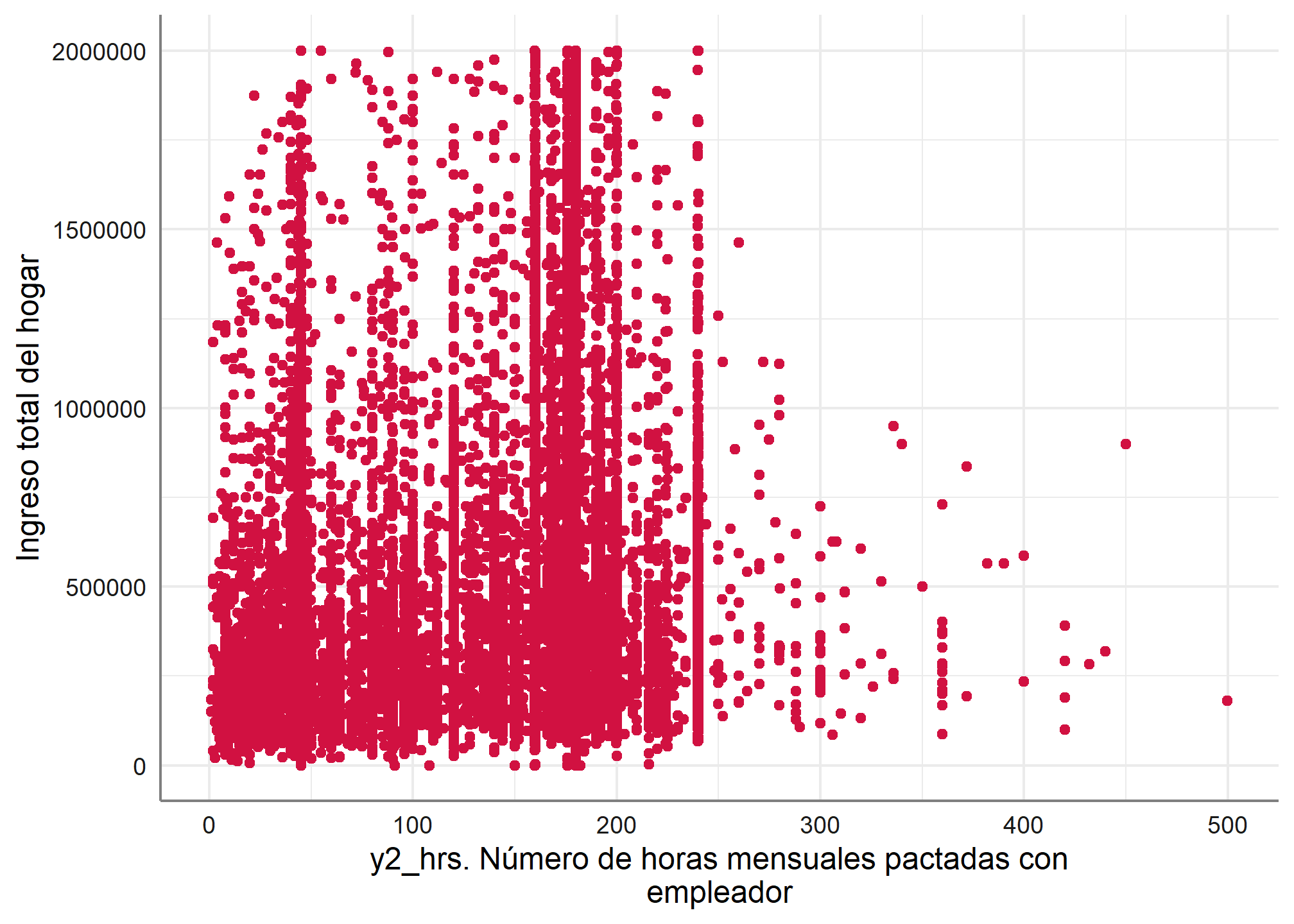
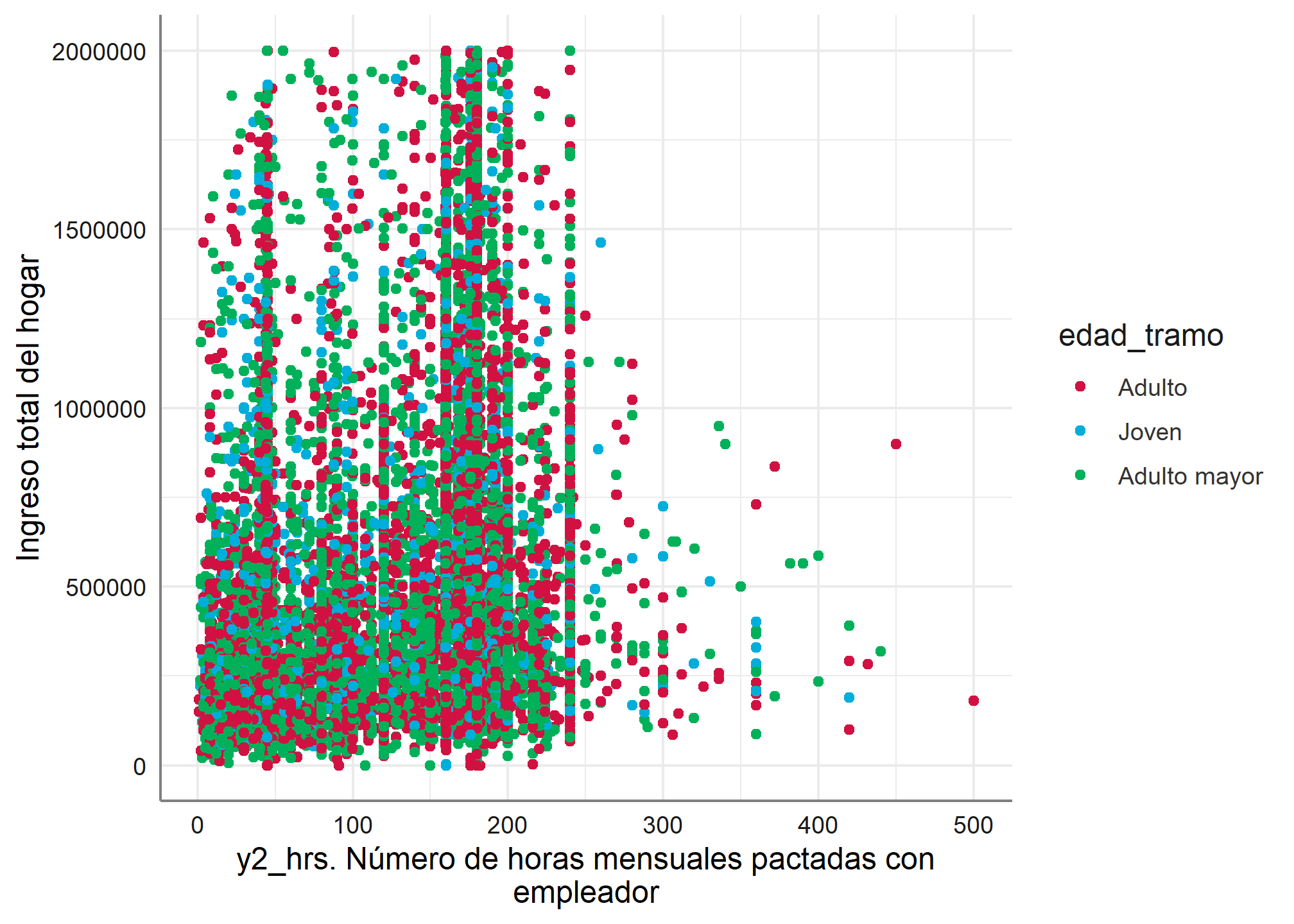
También es posible agregar una variable de ocupación al diagrama de dispersión.
datos_proc %>% filter(ingreso_percapita <= 2000000, horas_mens <= 600) %>%
plot_scatter(., horas_mens, ingreso_percapita, edad_tramo)
6. Visualización bivariada
Ahora que ya hemos graficado las frecuencias de las variables, vamos a graficar frecuencias agrupadas, para ello usaremos la función plot:grpfrq de sjPlot, su estructura es la siguiente
plot_grpfrq(
var.cnt,
var.grp,
type = c("bar", "dot", "line", "boxplot", "violin")
6.1 Gráfico de barras
La primera opción que nos entrega este código son los gráficos de barra, para usarlo queremos saber cuantos hombres y mujeres trabajaron al menos una hora la semana pasada, para ello graficaremos la variable sexo y ocupacion
plot_grpfrq(datos_proc$sexo, datos_proc$ocupacion,
type = c("bar"), title = "Gráfico de barras")
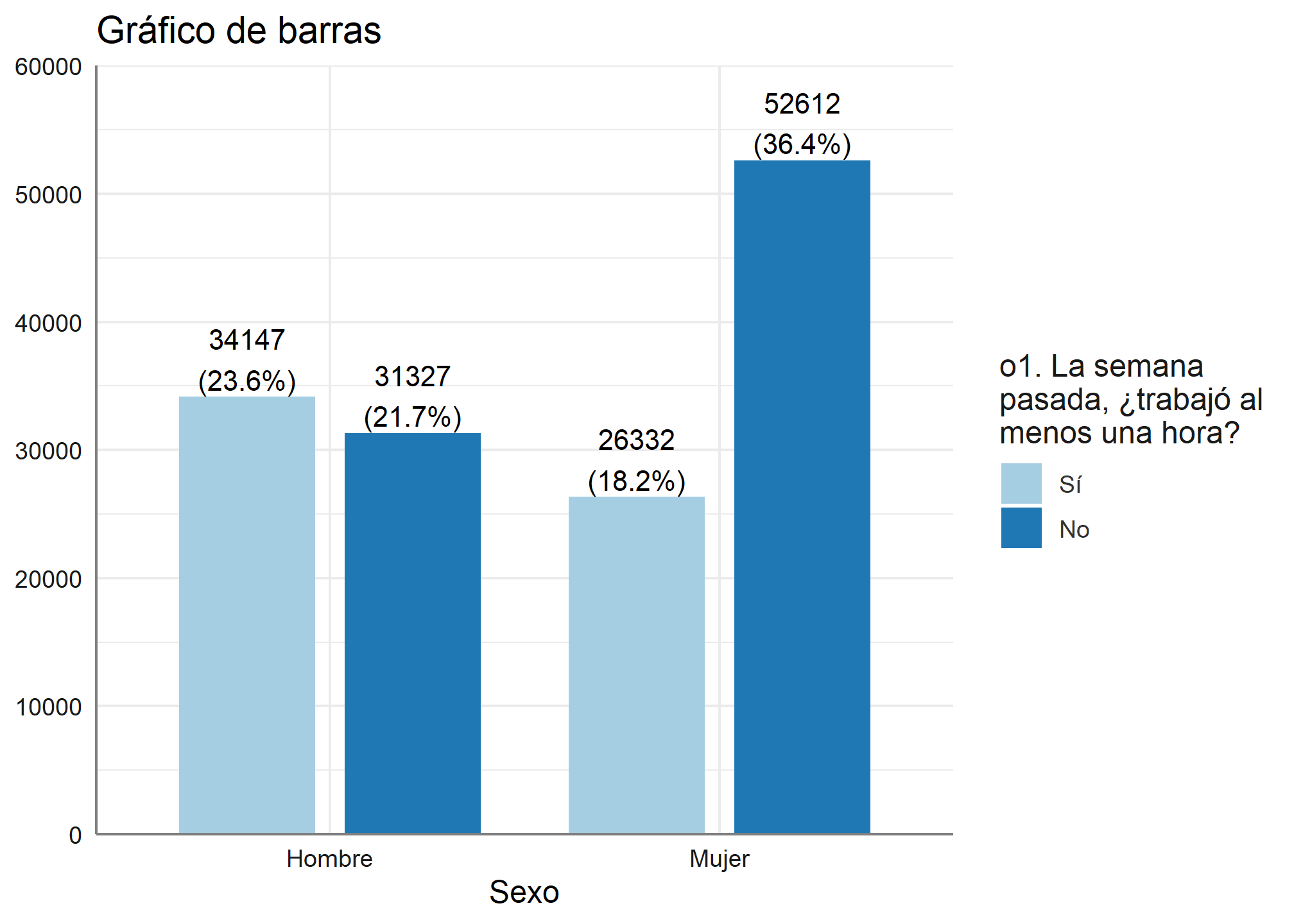
Podemos ver que no solo nos muestra la frecuencia absoluta, sino que también la relativa en porcentaje
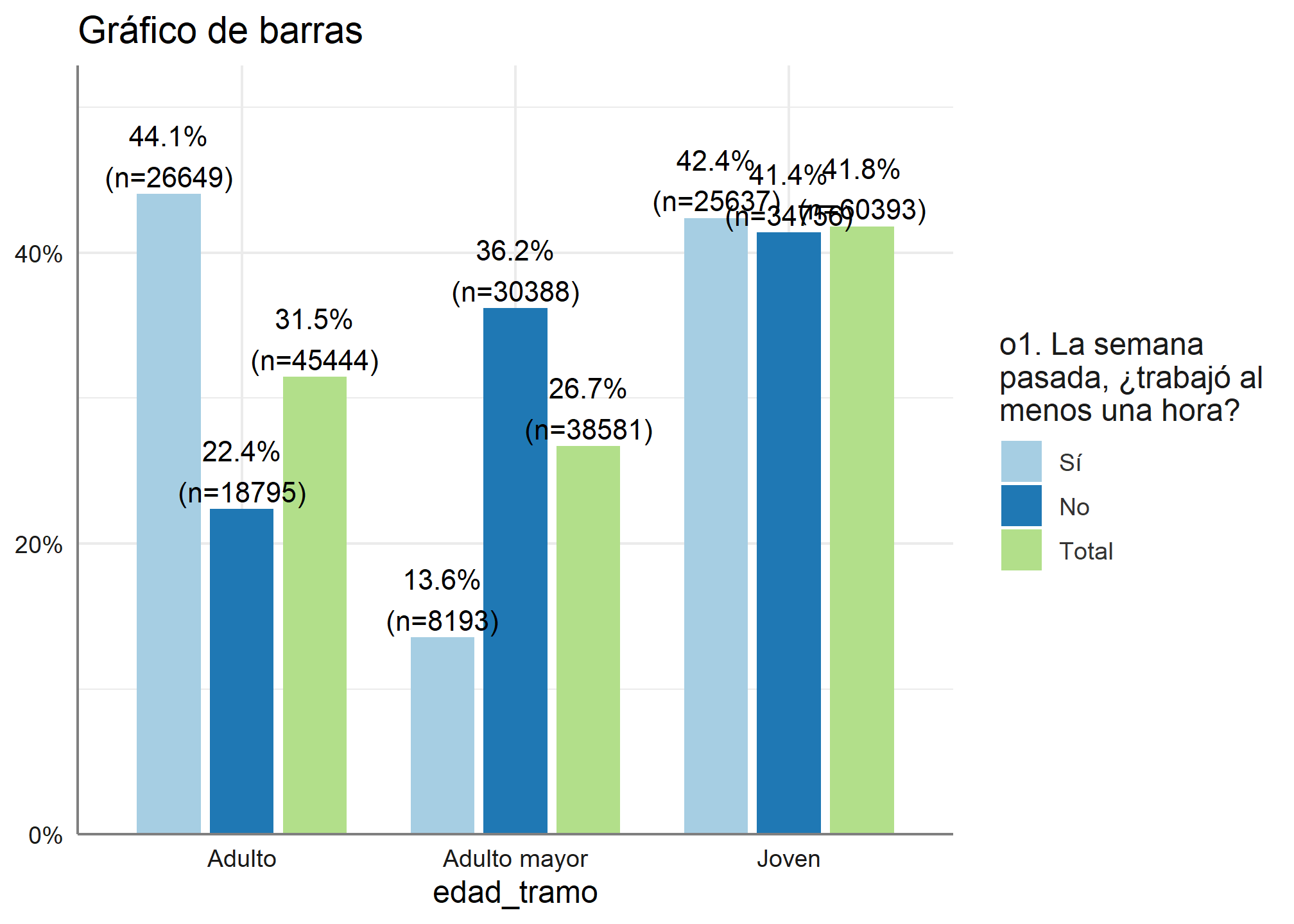
Pero además podemos ver agregar una tercera categoría, que es el total de ambas categorías. Para este ejercicio conoceremos que tramo de edad trabajo la semana pasada.
Para este ejercicio usaremos la función plot_xtab, de la misma librería
plot_xtab(datos_proc$edad_tramo, datos_proc$ocupacion, title = "Gráfico de barras")
6.2 Gráfico de barras horizontales
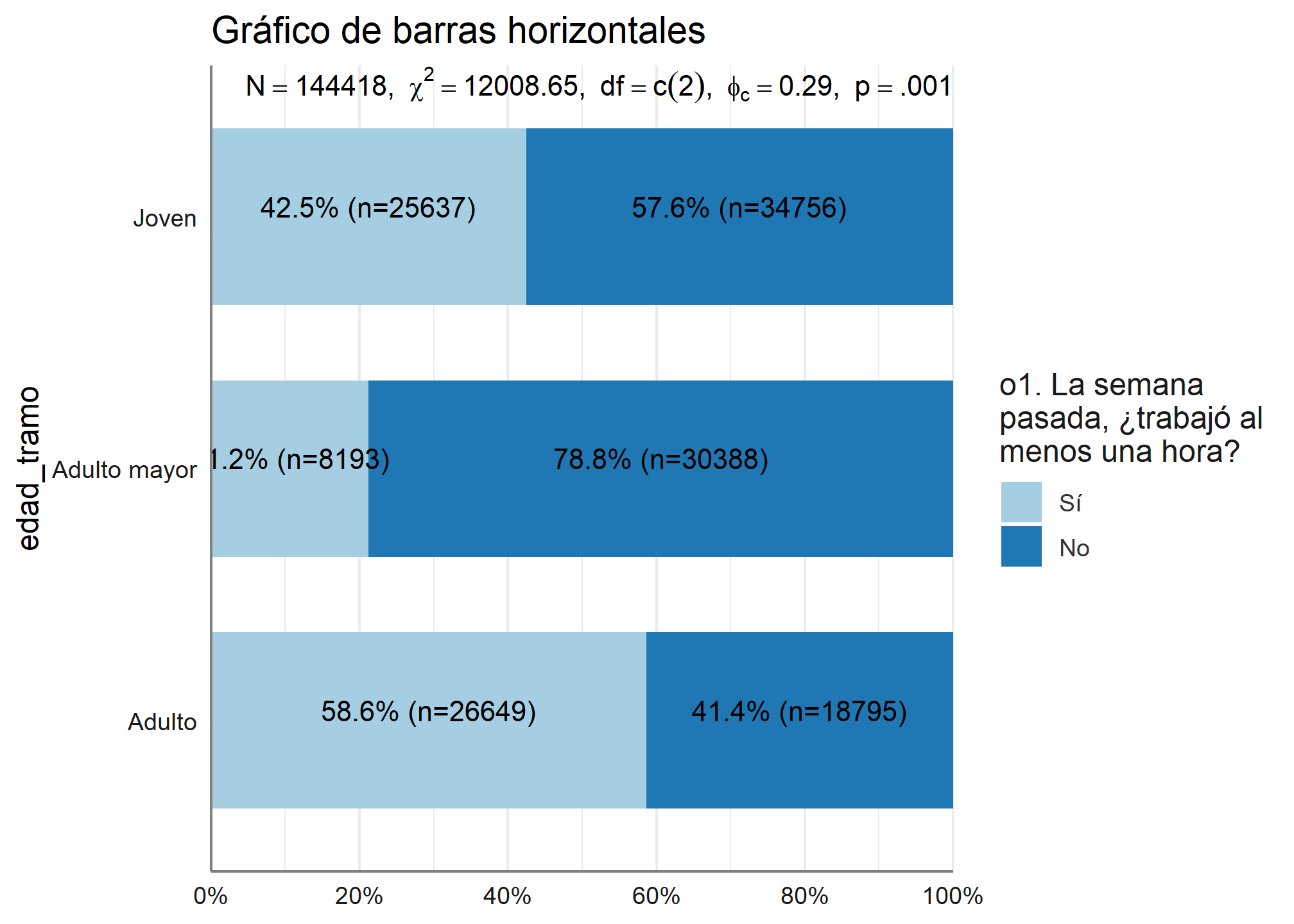
Con la misma función podemos graficar mediante barras horizontales
plot_xtab(datos_proc$edad_tramo, datos_proc$ocupacion, margin = "row",
bar.pos = "stack",
title = "Gráfico de barras horizontales",
show.summary = TRUE, coord.flip = TRUE)
6.3 Gráfico de líneas
Otra opción que tiene esta función, es la creación de gráficos de líneas, para ello conoceremos la relación entre el tramo etario y el recibir el IFE
plot_grpfrq(datos_proc$edad_tramo, datos_proc$ife,
title = "Gráfico de línea",
type = c("line"))
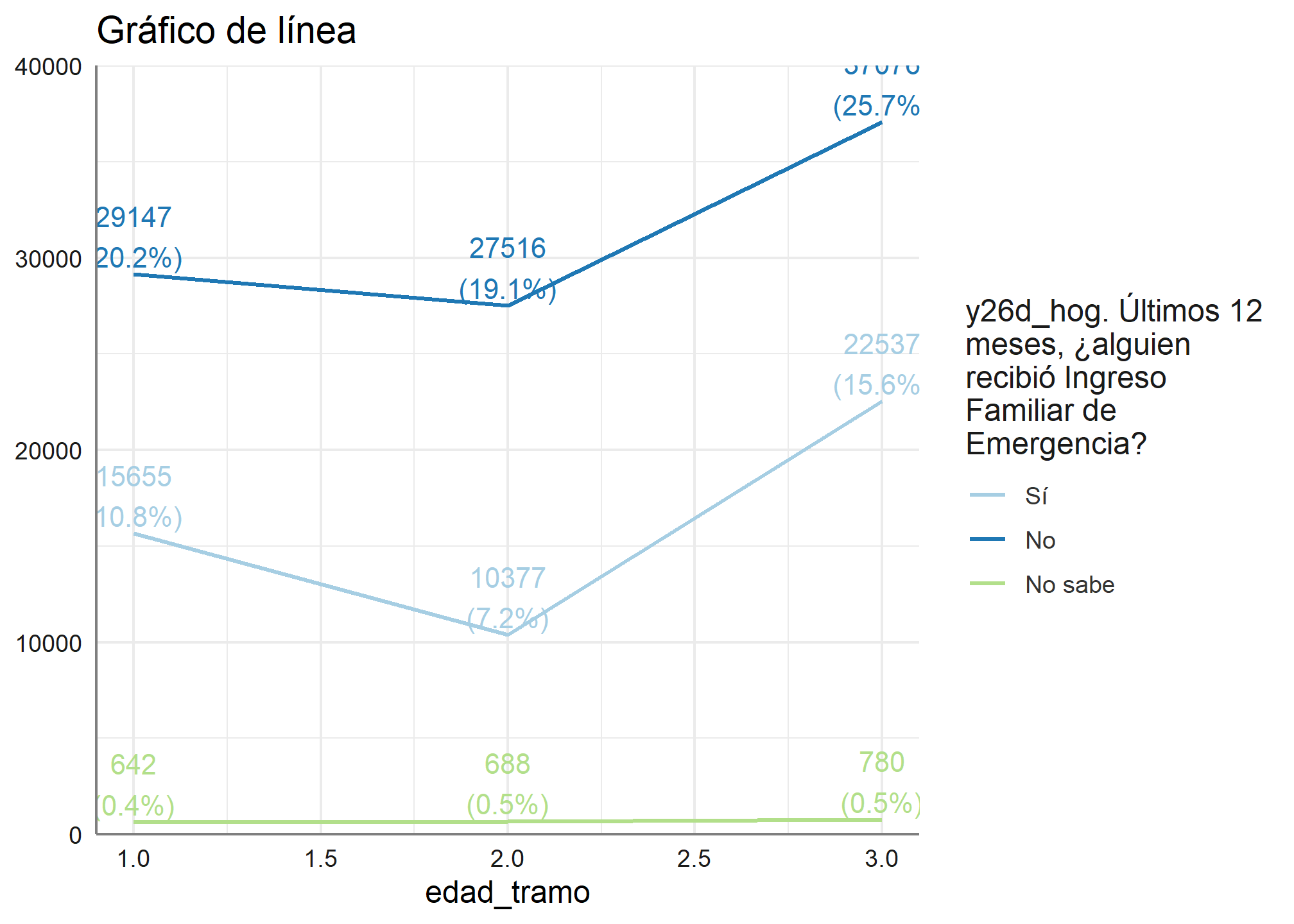
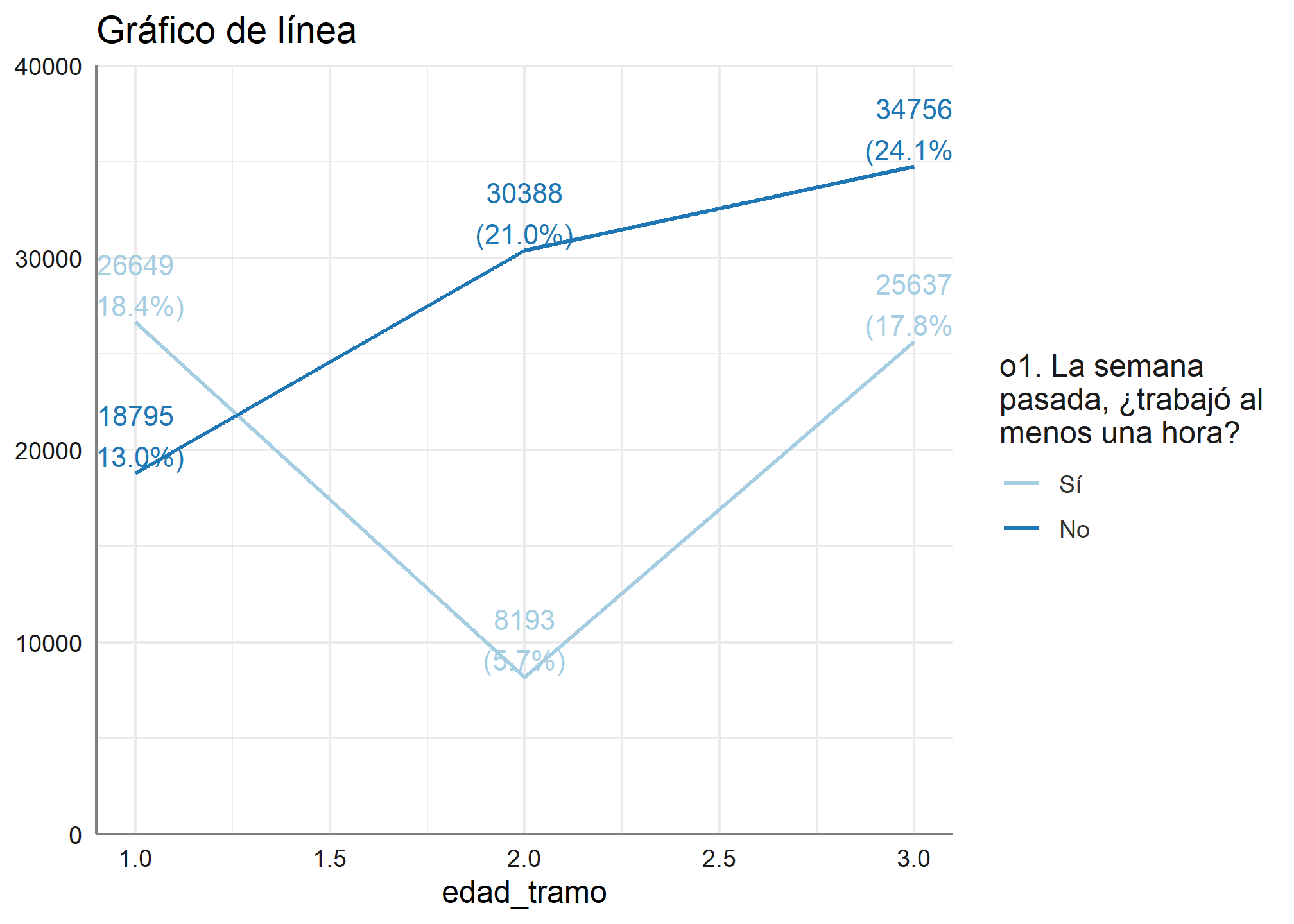
También podemos ver la relación de el tramo etario y si trabajó la semana pasada
plot_grpfrq(datos_proc$edad_tramo, datos_proc$ocupacion,
title = "Gráfico de línea",
type = "line")
6.4 Gráfico de cajas
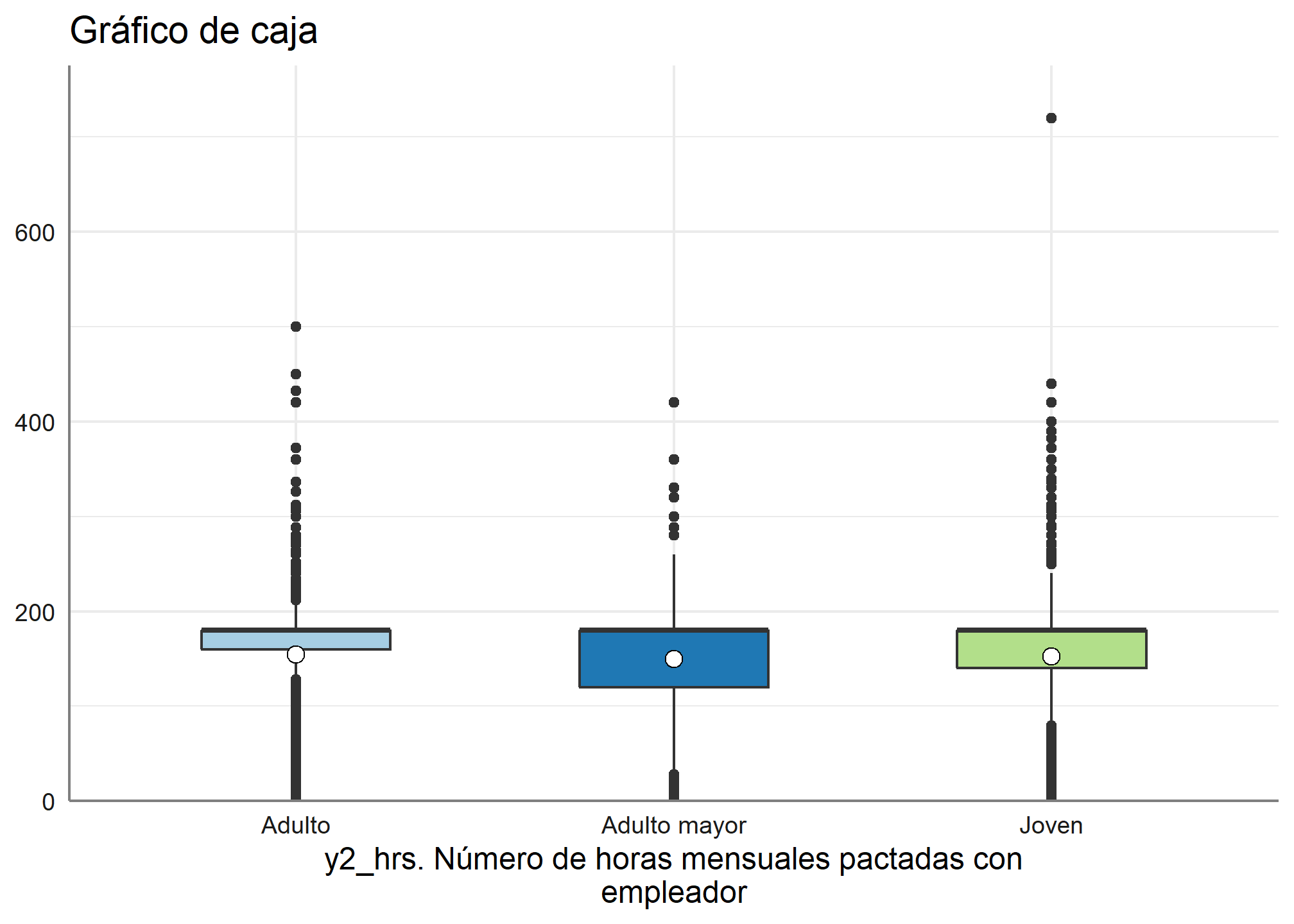
Ahora si queremos conocer cómo interactúa las horas de trabajo con el tramo etario, podemos visualizarlo mediante un gráfico de cajas
plot_grpfrq(datos_proc$horas_mens, datos_proc$edad_tramo,
title = "Gráfico de caja",
type = c("boxplot"))
Además, se puede incorporar una tercera variable, en este caso lo haremos con la variable sexo
plot_grpfrq(datos_proc$horas_mens, datos_proc$edad_tramo, intr.var = datos_proc$sexo,
title = "Gráfico de cajas",
type = "box")
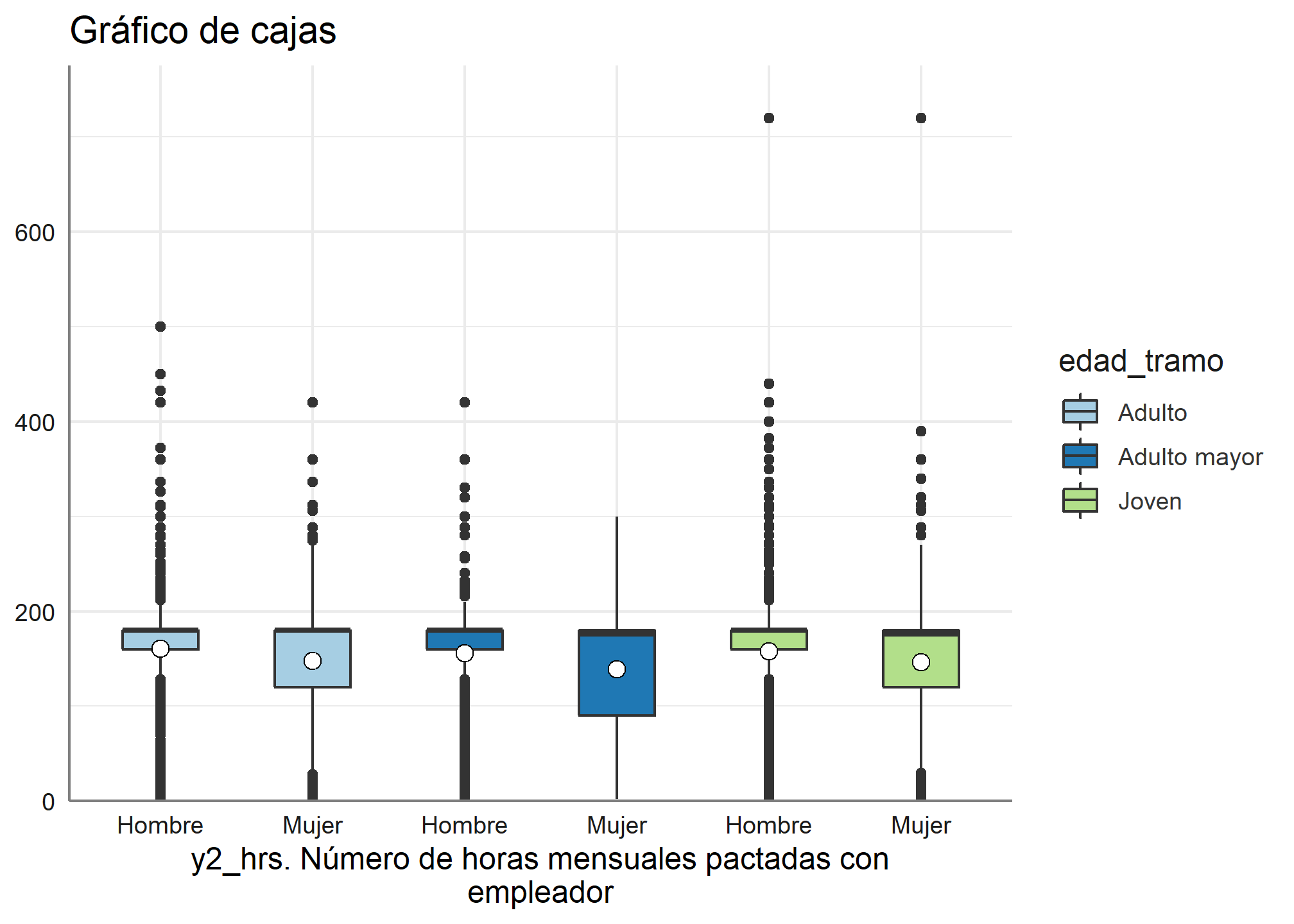
Nuevamente, la función nos permite la creación de múltiples gráficos, sólo se debe cambiar el argumento type =
7. Tablas de contingencia
¡No podemos terminar sin saber cómo hacer tablas de frecuencias cruzadas!
Por suerte sjPlot tiene la función sjt.xtab, que nos entrega tablas de frecuencias cruzadas
sjt.xtab(datos_proc$sexo, datos_proc$ife, title = "Tabla de contingencias",
show.col.prc=TRUE,
show.summary=FALSE)
| Sexo | y26d_hog. Últimos 12 meses, ¿alguien recibió Ingreso Familiar de Emergencia? |
Total | ||
|---|---|---|---|---|
| SÃ | No | No sabe | ||
| Hombre | 20958 43.2 % |
43550 46.5 % |
966 45.8 % |
65474 45.3 % |
| Mujer | 27611 56.8 % |
50189 53.5 % |
1144 54.2 % |
78944 54.7 % |
| Total | 48569 100 % |
93739 100 % |
2110 100 % |
144418 100 % |
¿Qué pasó? ¿por qué salen esos símbolos raros en la tabla?
¡Es por la codificación!, para ello le agregamos el argumento encoding = "UTF-8" y ya tenemos nuestra tabla de frecuencias cruzadas
sjt.xtab(datos_proc$sexo, datos_proc$ife,
show.col.prc=TRUE,
show.summary=FALSE,
encoding = "UTF-8",
title = "Tabla de contingencia",
file = "output/figures/tabla3.doc")
| Sexo | y26d_hog. Últimos 12 meses, ¿alguien recibió Ingreso Familiar de Emergencia? |
Total | ||
|---|---|---|---|---|
| SÃ | No | No sabe | ||
| Hombre | 20958 43.2 % |
43550 46.5 % |
966 45.8 % |
65474 45.3 % |
| Mujer | 27611 56.8 % |
50189 53.5 % |
1144 54.2 % |
78944 54.7 % |
| Total | 48569 100 % |
93739 100 % |
2110 100 % |
144418 100 % |
8. Correlación
Ahora veremos estadísticos bivariados, como la correlación, en esta ocasión generaremos una tabla de correlación entre las variables horas_mens y ingreso_percapita, para eso usaremos la función tab_corr de sjPlot
Previamente debemos seleccionar las variables a utilizar, ya que no tiene sentido incluir en el análisis variables nominales
datos_proc %>%
select(ingreso_percapita, horas_mens) %>%
tab_corr(.,
triangle = "lower",
title = "Tabla de correlación",
encoding = "UTF-8",
file = "output/figures/tabla4.doc")
| Ingreso total del hogar | y2_hrs. Número de horas mensuales pactadas con empleador |
|
|---|---|---|
| Ingreso total del hogar | ||
| y2_hrs. Número de horas mensuales pactadas con empleador |
0.054*** | |
| Computed correlation used pearson-method with listwise-deletion. | ||
9. Anova
Finalmente, si queremos reportar un análisis de Anova, no podemos dejar de lado este gráfico que nos otorga la función sjp.aov1 del paquete sjPlot
sjp.aov1(datos_proc$ingreso_percapita, datos_proc$sexo, title = "Anova")
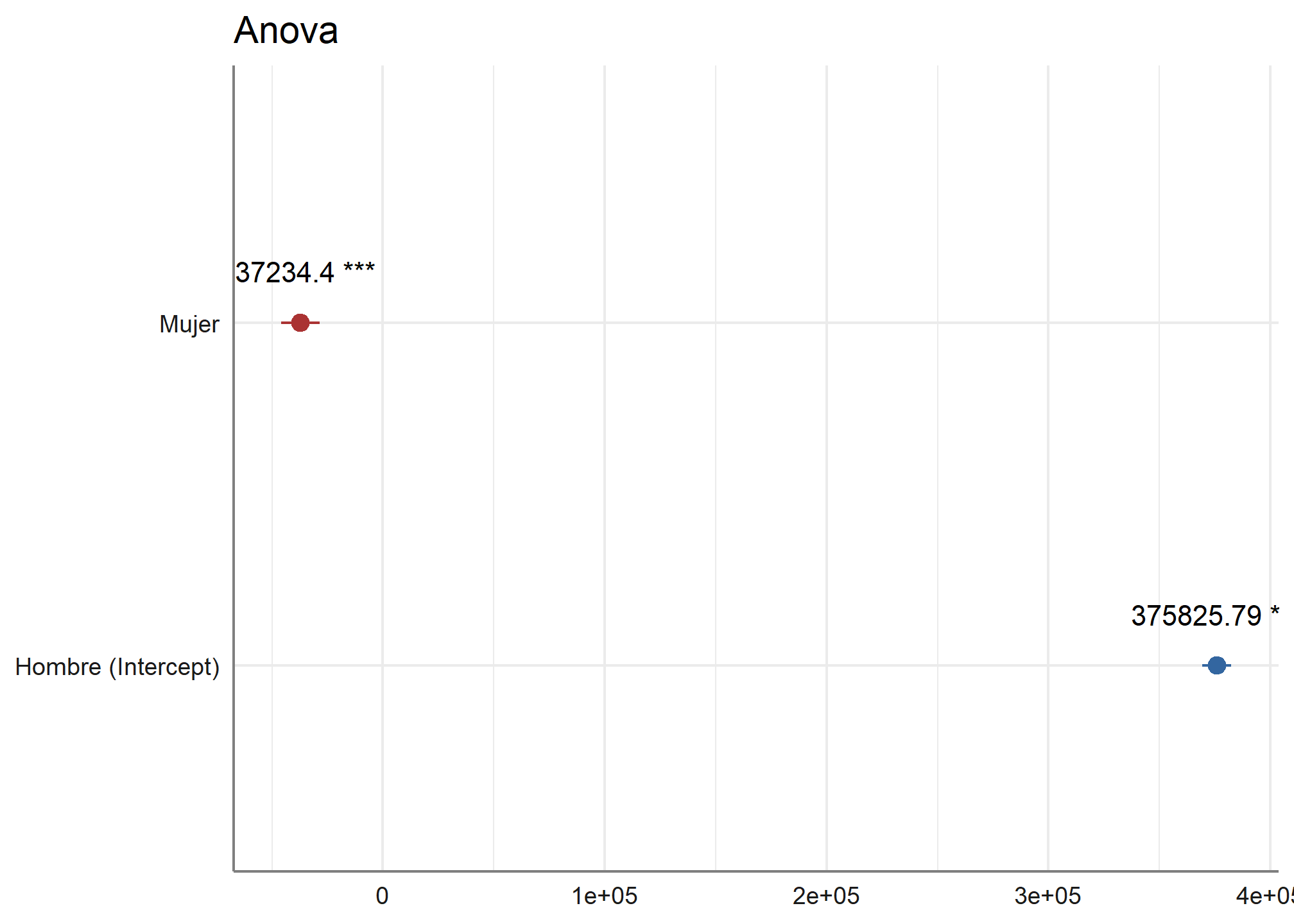
9. Resumen del práctico
¡Eso es todo por este práctico! Hoy aprendimos a:
- Manejar datos descriptivos en Rstudio
- A obtener tablas descriptivas
- A visualizar los descriptivos
- A obtener tablas de contingencia
- A obtener tablas de correlación
- A obtener gráficos de Anova
7. Reporte de progreso
¡Recuerda rellenar tu reporte de progreso. En tu correo electrónico está disponible el código mediante al cuál debes acceder para actualizar tu estado de avance del curso.